10.7 Constructing quadrilaterals
A quadrilateral is a closed polygon with four straight sides. Examples of quadrilaterals include squares, rectangles, parallelograms and rhombuses. In this section we will construct different quadrilaterals with a compass and ruler.
- quadrilateral
- a closed polygon that has four straight sides
A square is a quadrilateral with all sides equal in length and all interior angles equal to \(90^{\circ}\).
A rectangle is a quadrilateral with opposite sides equal in length and all interior angles equal to \(90^{\circ}\).
A parallelogram is a quadrilateral with opposite sides equal and parallel.
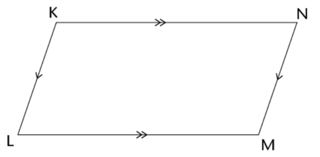
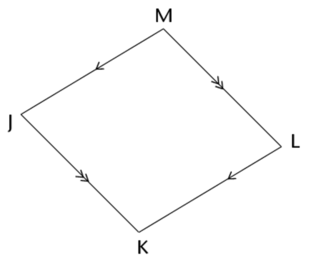
A rhombus is a quadrilateral with opposite sides parallel and all sides equal in length.
Worked Example 10.14: Constructing a square
Use a compass and a ruler to construct square \(ABCD\) with \(AB = 5 \text{ cm}\).
Construct \(AB = 5 \text{ cm}\) and \(\hat{A} = 90^{\circ}\).
Draw a line segment and mark point \(A\) on the line. Use a compass to measure a length of \(5 \text{ cm}\) on your ruler. Keeping the compass width the same, place the compass on point \(A\) and draw an arc that cuts the line. Label point \(B\). Use your compass to construct a \(90^{\circ}\) angle at point \(A\).
Construct lengths \(AD = 5\text{ cm}\) and \(BC = 5 \text{ cm}\).
Use your compass to measure a length of \(5 \text{ cm}\) on your ruler.
Keeping the compass width the same, place the compass on point \(A\) and draw an arc that cuts the perpendicular line. Label point \(D\).
Keeping the compass width the same, place the compass on point \(D\) and draw an arc above point \(B\).
Keeping the compass width the same, place your compass on \(B\) and draw an arc to intersect the other arc above \(B\). Label the point where the two arcs intersect point \(C\).
Draw line segments \(BC\) and \(CD\).
Use a ruler to draw sides \(BC\) and \(CD\) of square \(ABCD\).
Use your ruler to check the accuracy of the lengths of the sides and confirm that \(AB = BC = CD = DA = 5 \text{ cm}\).
Use a protractor to measure the interior angles of the square and confirm that \(\hat{A} = \hat{B} = \hat{C} = \hat{D} = 90^{\circ}\).
We can also construct quadrilaterals such as parallelograms and rhombuses using a compass. The following worked example demonstrates how to construct parallel lines.
Worked Example 10.15: Constructing parallel lines
Use a compass and a ruler to construct a pair of parallel lines.
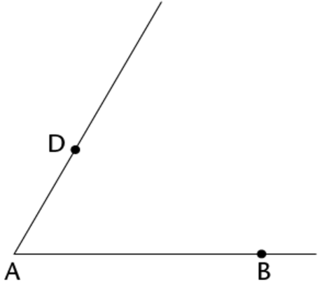
Draw line segments \(AB\) and \(AD\).
Use a ruler to draw line segments \(AB\) and \(AD\). Note that the point \(D\) will be on the line that will be parallel to \(AB\). Make sure to extend the line segment \(AD\) so that there is enough space for the construction.
Construct two arcs at points \(A\) and \(D\).
Set your compass to a width that is less than the length of \(AD\). Place the compass on point \(A\) and construct a wide arc that intersects \(AB\) and \(AD\). Keeping the width of the compass the same, place the compass on point \(D\) and construct another arc.
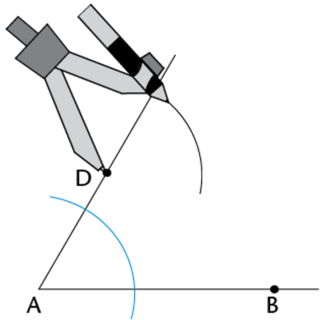
Set the compass to the width of the arc intersecting \(AB\) and \(AD\).
Set the compass width to the distance between the two points where the first arc crosses \(AB\) and \(AD\) (red dotted line).
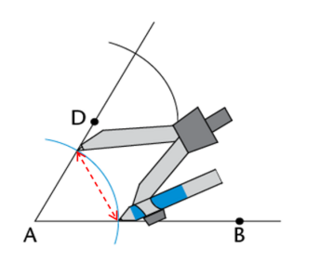
Keeping the compass width the same, place the compass on the point where the second arc crosses \(AD\) and draw a third arc that intersects the second arc.
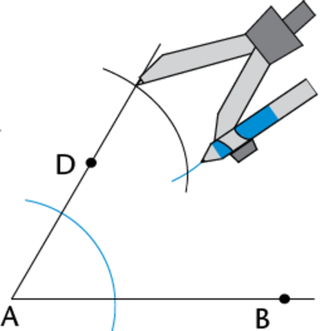
Draw a line that passes through \(D\) and is parallel to \(AB\).
Draw a line from point \(D\) and through the point where the two arcs intersect.
This constructed line is parallel to \(AB\).

Worked Example 10.16: Constructing a parallelogram
Use a compass and a ruler to construct parallelogram \(PQRS\) with \(PQ = 4 \text{ cm}, QR = 3 \text{ cm}\) and \(S\hat{P}Q = 45^{\circ}\).
Construct \(PQ = 4 \text{ cm}\) and \(\hat{P} = 90^{\circ}\).
Draw a line segment and mark point \(P\) on the line. Use a compass to measure a length of \(4 \text{ cm}\) on your ruler. Keeping the compass width the same, place the compass on point \(P\) and draw an arc that cuts the line. Label point \(Q\).
Use your compass to construct a \(90^{\circ}\) angle at point \(P\).
Bisect the right angle at \(P\).
Use your compass to bisect the right angle at \(P\) to get \(S\hat{P}Q = 45^{\circ}\).
Construct \(PS = 3 \text{ cm}\).
Use your compass to measure a length of \(3 \text{ cm}\) on your ruler.
Keeping the compass width the same, place the compass on point \(P\) and draw an arc that intersects the \(45^{\circ}\) line. Label point \(S\).
Keeping the compass width the same, place the compass on point \(Q\) and draw an arc above point \(Q\).
Construct \(QR\) and \(RS\)
Use your compass to measure a length of \(4 \text{ cm}\) on your ruler.
Keeping the compass width the same, place the compass on point \(S\) and draw an arc that cuts the arc above point \(Q\). Label the point of intersection \(R\).
Draw line segments \(QR\) and \(RS\).
Use your ruler to check the accuracy of the lengths of the sides and confirm that \(PQ = SR = 4 \text{ cm}\) and \(QR = PS = 3 \text{ cm}\).
Use a protractor to measure and confirm that \(S\hat{P}Q = 45^{\circ}\).
Construct quadrilaterals
Use a compass and a ruler to construct square \(MNPQ\) with \(MN = \text{4,5} \text{ cm}\).
Use a compass and a ruler to construct parallelogram \(JKLM\) using the parallel lines method.
Use a compass and a ruler to construct rectangle \(ABCD\) with \(AB = 8 \text{ cm}\) and \(BC = \text{3,5} \text{ cm}\).
Use a compass and a ruler to construct parallelogram \(WXYZ\) with \(WX = 7 \text{ cm}\) and \(XY = 4 \text{ cm}\) and \(Z\hat{W}X = 60^{\circ}\).
Use a compass and a ruler to construct rhombus \(PQRS\) with \(PQ = 6 \text{ cm}\) and \(S\hat{P}Q = 45^{\circ}\).
Use a compass and a ruler to construct parallelogram \(QRST\) with \(QR = 5 \text{ cm}\) and \(RS = \text{6,5} \text{ cm}\) and \(T\hat{Q}R = 30^{\circ}\).
