6.4 Evaluating algebraic expressions
The most important idea behind evaluating algebraic expressions is the idea of substitution. We substitute (or replace) the unknown variables with known values and calculate the new value or evaluate the expression. This process often leads to finding a single numerical value, which is the result of calculations determined by the algebraic expression.
- substitute
- to replace a variable in an equation with a value
We can think about this process as a flow diagram of input values. For example, to calculate the numerical value of \(10x + 2y\) for \(x = 3\) and \(y = 2\), we can complete the empty spaces in the diagram.
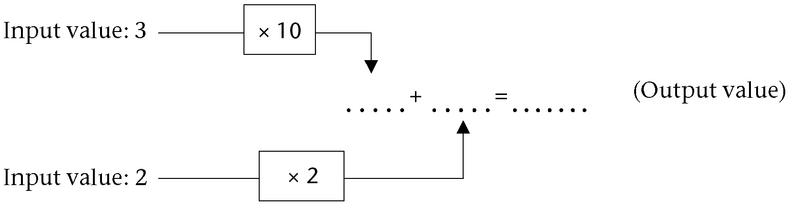
The first output is \(30\) and the second output is \(4\). Adding the two outputs together will give us the value of the expression:
\[10x + 2y\] \[= 10(3) + 2(2)\] \[= 30 + 4\] \[= 34\]Remember that terms are separated by addition and subtraction symbols, and are joined into one by multiplication symbols, division symbols, and brackets. To evaluate an expression, we must:
- separate it into terms
- simplify each term (if needed)
- add or subtract from left to right.
Worked example 6.11: Evaluating expressions
Evaluate the following expression if \(y = 8\), without using a calculator:
\[3 + 4y\]Substitute.
Substitute \(y = 8\) into the expression.
Always use brackets when substituting.
\[3 + 4y\] \[= 3 + 4(8)\]Calculate the value.
This expression has two terms:
\[= 3 + 4(8)\] \[= 3 + 32\] \[= 35\]Therefore, the value of the expression when \(y = 8\) is \(35\).
Worked example 6.12: Evaluating expressions
Evaluate the following expression if \(y = 2\), without using a calculator:
\[2y^{2} - 5y + 5\]Substitute \(y = 2\) into the expression.
Hint: Always use brackets when substituting.
\[2y^{2} - 5y + 5\] \[= 2(2)^{2} - 5(2) + 5\]Evaluate the exponent term and simplify.
Exponents come before multiplication: \(2(2)^{2} = 2(2)(2) = 2(4)\).
\[= 2(4) - 10 + 5\] \[= 8 - 10 + 5\] \[= - 2 + 5\] \[= 3\]Therefore the value of the expression when \(y = 2\) is \(3\).
Worked example 6.13: Evaluating expressions
Evaluate the following expression if \(a = 4\) and \(b = - 2\), without using a calculator:
\[- 3a + ab^{2}\]Substitute.
Substitute \(a = 4\) and \(b = - 2\) into the expression.
Remember to use brackets when substituting.
\[- 3a + ab^{2}\] \[= - 3(4) + (4)( - 2)^{2}\]Evaluate the exponent term and simplify.
Exponents come before multiplication: \(4( - 2)^{2} = 4( - 2)( - 2) = 4(4)\).
\[= - 12 + 4(4)\] \[= - 12 + 16\] \[= 4\]Therefore the value of the expression when \(a = 4\) and \(b = - 2\) is \(4\).
Restrictions in algebraic expressions
When working with algebraic expressions that contain fractions, it is always important to check whether there are variables in the denominator. An expression is undefined when we try to divide by zero (in other words, when zero is in the denominator of a fraction).
Similarly, when working with square roots, it is important to pay attention to the variables under the square root. An expression is undefined when we try to take a square root of a negative number.
For example, in the case of an algebraic fraction \(\frac{2}{a - 1}\) we can see that \(a - 1\) can never be equal to 0 because this avoids division by zero and having the expression undefined. So, \(a - 1 \neq 0\) and this means that \(a \neq 1\). We need to exclude the value of \(1\) from the set of numbers we are able to substitute into the given expression. In other words, the expression \(\frac{2}{a - 1}\) is defined for all real values except \(1\).
In another example, with the square root \(1 + \sqrt{a - 2}\), we have to make sure that \(a - 2 \geq 0\), because the square root of a negative number is undefined. So, \(a - 2 \geq 0\) and \(a \geq 2\). We will exclude all the numbers that are less than \(2\) from the set of numbers we are able to substitute into the given expression. In other words, the expression, \(1 + \sqrt{a - 2}\), is defined for all real values except \(a < 2\).
Worked example 6.14: Domain of algebraic expressions
Consider the following expression:
\[\frac{kj^{3}}{j - 4} - 3k^{2}\]- For which value of \(j\) is the expression undefined?
- Evaluate the expression when \(j = - 4\) and \(k = - 1\), without using a calculator.
Determine the value(s) of \(j\) that will make the expression undefined.
Looking at the expression, we can see that \(j\) is in the denominator of the first term:
\[\frac{kj^{3}}{j - 4} - 3k^{2}\]The expression will be undefined when \(j - 4 = 0\).
\[(4) - 4 = 0\]Therefore, the expression will be undefined when \(j = 4\).
Evaluate the expression when \(j = - 4\) and \(k = - 1\), without using a calculator.
Remember to use brackets when substituting the values for variables!
Evaluate the exponents and simplify. Exponents come before multiplication:
- \(kj^{3} = ( - 1)( - 4)^{3} = ( - 1)( - 4)( - 4)( - 4) = ( - 1)( - 64)\)
- \(3k^{2} = - 3( - 1)^{2} = - 3( - 1)( - 1) = - 3(1)\)
So, the value of the expression when \(j = - 4\) and \(k = - 1\) is \(11\).
Worked example 6.15: Algebraic expressions with square roots
If \(x = 3\), determine the value of this expression:
\[\sqrt{2x + 3}\]Evaluate inside the root.
To find the answer, you need to substitute these numbers into the expression and follow BOEDMAS until you are done with all of the calculations.
Start by working out the expression inside of the root; then you can evaluate the root itself. The reason for this is that a root acts like a pair of brackets. In other words, there are “invisible” brackets inside of every root. It is a good idea to draw brackets into the expression like this:
\[\sqrt{2x + 3} = \sqrt{(2x + 3)}\]BOEDMAS tells you that you must do the operations inside of the brackets first.
Substitute the numbers into the expression.
Do not do anything with the square root yet. Just copy it in each line while you are working on the inside.
\[\sqrt{(2x + 3)}\] \[= \sqrt{\left( 2(3) + 3 \right)}\] \[= \sqrt{(6 + 3)}\] \[= \sqrt{9}\]Remember, if the number under the square root is negative, then the value of the expression is undefined.
Evaluate the square root.
At this point, there is only one step remaining: evaluate the square root. Luckily, \(9\) is a square number, so the answer is nice and tidy.
\[\sqrt{9} = 3\]The answer is \(3\).
Special algebraic expressions
When working with exponents, the principle of substitution is the same: replace the variable with the input number and calculate the result.
If 𝑛 is a natural number, then \(3^{n}\) is a formula that always gives powers of three.
| \(n\) | \(3^{n}\) |
|---|---|
| \(1\) | \(3^{1} = 3\) |
| \(2\) | \(3^{2} = 3 \times 3 = 9\) |
| \(3\) | \(3^{3} = 3 \times 3 \times 3 = 27\) |
The values that we get out for \(3^{n}\) are all powers of three.
A power of three is a number that is found by raising \(3\) to the power of some whole number.
If \(n\) is a natural number, then \(n^{3}\) is a formula that always gives perfect cubes:
| \(n\) | \(n^{3}\) |
|---|---|
| \(1\) | \((1)^{3} = 1 \times 1 \times 1 = 1\) |
| \(2\) | \((2)^{3} = 2 \times 2 \times 2 = 8\) |
| \(3\) | \((3)^{3} = 3 \times 3 \times 3 = 27\) |
The values that we get for \(n^{3}\) are all perfect cubes.
A perfect cube is a number that is found by cubing a whole number.
So, \(n^{3}\) will be a perfect cube for all natural number values of \(n\).
Therefore, \(n^{3}\) is a formula that always gives perfect cubes.
Other special formulae:
- If 𝑛 is a natural number, then \(2n\) is a formula that always gives even numbers.
- If 𝑛 is a natural number, then \(2n - 1\) is a formula that always gives odd numbers.
- To get consecutive natural numbers, we start with a natural number and add 1 each time. For example, if we start at \(n\), the next consecutive natural number is \(n + 1\).
Worked example 6.16: Consecutive numbers
The formula for powers of the number \(2\) is \(2^{n}\), where \(n\) is a whole number. The list of consecutive natural numbers is \(n\); \(n + 1\); \(n + 2\).
Write the formula for three consecutive powers of the number \(2\) in terms of \(n\). Check your answer for all three powers.
Find the formula.
If we start at \(n\), the next consecutive natural number is \(n + 1\).
We add \(1\) again to get the following consecutive natural number: \((n + 1) + 1 = n + 2\).
The list of consecutive natural numbers is \(n\); \(n + 1\); \(n + 2\).
Therefore the list of expressions for consecutive powers of the number \(2\) is: \(2^{n}\); \(2^{n + 1}\); \(2^{n + 2}\)
Write three powers of the number \(2\) using the formula.
If \(n = 3\), then \(2^{n}\); \(2^{n + 1}\); \(2^{n + 2}\) looks like this:
\(2^{3}\); \(2^{3 + 1}\); \(2^{3 + 2}\)
\[2^{3};2^{4};2^{5}\] \[8;16;32\]This is a list of consecutive powers of the number \(2\), because there are no powers of the number \(2\) between these numbers.
